Skip to content

Hierarchical CWE Scoring System (HCSS)

Below is a proposal for a comprehensive scoring system for evaluating automated CVE-to-CWE assignments that addresses both the multi-label nature of the problem and the hierarchical structure of the CWE framework.

See A survey of Hierarchical Classification Standards for background context.

1. Core Design Principles

The Hierarchical CWE Scoring System (HCSS) is designed with the following principles:

  1. Handle Multi-Label Classification: Support evaluating cases where a CVE has multiple correct CWE labels
  2. Leverage Hierarchy: Use the CWE hierarchy to award partial credit based on semantic proximity
  3. Balanced Evaluation: Provide metrics that balance precision and recall
  4. Standardized Scoring: Deliver scores in an interpretable range (0-1)
  5. Comparability: Align with established evaluation practices in hierarchical classification

2. HCSS Methodology

2.1 Set Augmentation Approach

HCSS uses a set augmentation approach based on established hierarchical classification research:

  1. For each CVE, we have:
  2. Y: The set of true/benchmark CWE identifiers

  3. Ŷ: The set of predicted CWE identifiers

  4. We augment both sets with all ancestors in the CWE hierarchy:

  5. \(Y_aug = Y ∪\) {all ancestors of each CWE in Y}

  6. \(Ŷ_aug = Ŷ ∪\) {all ancestors of each CWE in Ŷ}

  7. Calculate hierarchical precision (hP), recall (hR), and F-measure (hF) using set operations:

$$ hP = |Ŷ_aug ∩ Y_aug| / |Ŷ_aug| $$

$$ hR = |Ŷ_aug ∩ Y_aug| / |Y_aug| $$

$$hF = 2 × hP × hR / (hP + hR) $$

2.2 Aggregation Methods

For a dataset containing multiple CVEs, HCSS calculates two types of averages:

  1. Micro-average: Aggregates the numerators and denominators across all CVEs before division
  2. Gives more weight to CVEs with more complex mappings

  3. Reflects overall performance

  4. Macro-average: Calculates metrics for each CVE separately and then averages

  5. Gives equal weight to each CVE
  6. Shows performance across different types of vulnerabilities

The primary results to be reported are Micro-hF and Macro-hF, along with the constituent hP and hR values.

3. Implementation Details

3.1 Ancestor Calculation

To determine ancestors for a CWE node: 1. Parse the MITRE CWE XML data to build the hierarchy graph 2. For each node, recursively traverse up all "ChildOf" relationships to identify all ancestors 3. Store the ancestors for efficient lookup during scoring

3.2 Handling Special Cases

  • Empty sets: If Y or Ŷ is empty, handle accordingly (0 for precision when Ŷ is empty, 0 for recall when Y is empty)
  • Root node: The root node CWE-1000 is not included in the comparison sets.
  • If it was, it would result in overly generous partial credit even for a complete mismatch, since there is always 1 element (the root) common in both sets
  • Different views: The CWE can be viewed through different perspectives (e.g., CWE-1000 per https://riskbasedprioritization.github.io/cwe/cwe_views/) which should be used for evaluation.

4. Worked Examples

Example 1: Single CWE, Exact Match

  • Benchmark: CWE-79

  • Prediction: CWE-79

  • Augment sets (actual hierarchy: CWE-79 → CWE-74 → CWE-707 → CWE-1000, but excluding CWE-1000):

  • Y_aug = {CWE-79, CWE-74, CWE-707}

  • Ŷ_aug = {CWE-79, CWE-74, CWE-707}

  • Calculate metrics:

  • hP = |{CWE-79, CWE-74, CWE-707}| / |{CWE-79, CWE-74, CWE-707}| = 3/3 = 1.0

  • hR = |{CWE-79, CWE-74, CWE-707}| / |{CWE-79, CWE-74, CWE-707}| = 3/3 = 1.0
  • hF = 2 × 1.0 × 1.0 / (1.0 + 1.0) = 1.0

Result: Perfect score (1.0) for exact match.

Example 2: Single CWE, Parent Relationship

  • Benchmark: CWE-79

  • Prediction: CWE-74 (direct parent of CWE-79)

  • Augment sets (using the hierarchy: CWE-79 → CWE-74 → CWE-707, excluding CWE-1000):

    • Ancestors of CWE-79 are CWE-74 and CWE-707.
    • Y_aug (Benchmark set) = {CWE-79, CWE-74, CWE-707}
    • Ancestors of CWE-74 are CWE-707.
    • Ŷ_aug (Prediction set) = {CWE-74, CWE-707}

  • Calculate metrics:

    • Intersection: \(Y_{aug} \cap \hat{Y}_{aug} = \{CWE-79, CWE-74, CWE-707\} \cap \{CWE-74, CWE-707\} = \{CWE-74, CWE-707\}\)
    • Precision (hP): $$ \frac{|{CWE-74, CWE-707}|}{|{CWE-74, CWE-707}|} = \frac{2}{2} = 1.0 $$
    • Recall (hR): $$ \frac{|{CWE-74, CWE-707}|}{|{CWE-79, CWE-74, CWE-707}|} = \frac{2}{3} \approx 0.667 $$
    • F-score (hF): $$ \frac{2 \times 1.0 \times 0.667}{(1.0 + 0.667)} = \frac{1.334}{1.667} \approx 0.800 $$

Result: High but not perfect score (0.800) for predicting a direct parent.

Example 3: Single CWE, No Match

  • Benchmark: CWE-79

  • Prediction: CWE-352 (unrelated to CWE-79)

  • Augment sets (excluding CWE-1000):

    • Ancestors of CWE-79: CWE-79 → CWE-74 → CWE-707
    • Ancestors of CWE-352: CWE-352 → CWE-345 → CWE-693
    • Y_aug = {CWE-79, CWE-74, CWE-707}
    • Ŷ_aug = {CWE-352, CWE-345, CWE-693}

  • Calculate metrics:

    • hP = |{}| / |{CWE-352, CWE-345, CWE-693}| = 0/3 = 0.0
    • hR = |{}| / |{CWE-79, CWE-74, CWE-707}| = 0/3 = 0.0
    • hF = 0.0 (by definition when precision and recall are zero)

Result: Complete mismatch (0.0).

Example 4: Single CWE, Parent Relationship

  • Benchmark: CWE-79

  • Prediction: CWE-74 (direct parent of CWE-79)

  • Augment sets (excluding CWE-1000):

    • Y_aug = {CWE-79, CWE-74, CWE-707}
    • Ŷ_aug = {CWE-74, CWE-707}

  • Calculate metrics:

    • hP = |{CWE-74, CWE-707}| / |{CWE-74, CWE-707}| = 2/2 = 1.0
    • hR = |{CWE-74, CWE-707}| / |{CWE-79, CWE-74, CWE-707}| = 2/3 ≈ 0.667
    • hF = 2 × 1.0 × 0.667 / (1.0 + 0.667) ≈ 1.334 / 1.667 ≈ 0.800

Result: High but not perfect score (0.800) for parent prediction.

Example 5: Complex Multi-Label Case

  • Benchmark: CWE-79, CWE-89

  • Prediction: CWE-79, CWE-74, CWE-352

  • Augment sets (using the provided chains, excluding CWE-1000):

    • Ancestors of CWE-79: CWE-79 → CWE-74 → CWE-707
    • Ancestors of CWE-89: CWE-89 → CWE-943 → CWE-74 → CWE-707
    • Ancestors of CWE-352: CWE-352 → CWE-345 → CWE-693

Thus:

  • Y_aug (Benchmark set) = {CWE-79, CWE-89, CWE-74, CWE-707, CWE-943}

  • Ŷ_aug (Prediction set) = {CWE-79, CWE-74, CWE-707, CWE-352, CWE-345, CWE-693}

  • Calculate metrics:

  • Intersection: {CWE-79, CWE-74, CWE-707}

  • Precision (hP):
\[ \frac{| \{CWE-79, CWE-74, CWE-707\} |}{| \{CWE-79, CWE-74, CWE-707, CWE-352, CWE-345, CWE-693\} |} = \frac{3}{6} = 0.500 \]
  • Recall (hR):
\[ \frac{| \{CWE-79, CWE-74, CWE-707\} |}{| \{CWE-79, CWE-89, CWE-74, CWE-707, CWE-943\} |} = \frac{3}{5} = 0.600 \]
  • F-score (hF):
\[ \frac{2 \times 0.500 \times 0.600}{(0.500 + 0.600)} = \frac{0.600}{1.100} \approx 0.545 \]

Result: Moderate score (0.545) due to correctly predicting CWE-79 and its ancestors but failing to predict CWE-89 and adding unrelated CWEs (CWE-352).

Example 6: Complex Multi-Label Case with Missing and Partial Matches

  • Benchmark: CWE-79, CWE-89, CWE-352

  • Prediction: CWE-79, CWE-74

  • Augment sets (using provided hierarchy, excluding CWE-1000):

    • Ancestors of CWE-79: CWE-79 → CWE-74 → CWE-707
    • Ancestors of CWE-89: CWE-89 → CWE-943 → CWE-74 → CWE-707
    • Ancestors of CWE-352: CWE-352 → CWE-345 → CWE-693

Thus:

  • Y_aug (Benchmark set) = {CWE-79, CWE-89, CWE-352, CWE-74, CWE-707, CWE-943, CWE-345, CWE-693}

  • Ŷ_aug (Prediction set) = {CWE-79, CWE-74, CWE-707}

  • Calculate metrics:

  • Intersection: {CWE-79, CWE-74, CWE-707}

  • Precision (hP):
\[ \frac{| \{CWE-79, CWE-74, CWE-707\} |}{| \{CWE-79, CWE-74, CWE-707\} |} = \frac{3}{3} = 1.0 \]
  • Recall (hR):
\[ \frac{| \{CWE-79, CWE-74, CWE-707\} |}{| \{CWE-79, CWE-89, CWE-352, CWE-74, CWE-707, CWE-943, CWE-345, CWE-693\} |} = \frac{3}{8} = 0.375 \]
  • F-score (hF):
\[ \frac{2 \times 1.0 \times 0.375}{(1.0 + 0.375)} = \frac{0.75}{1.375} \approx 0.545 \]

Result: Moderate score (0.545) reflecting precise but incomplete prediction—correctly capturing CWE-79 but missing CWE-89, CWE-352..

Example 7: Complex Multi-Label Case with Multiple Paths and Partial Matches

CWE-798 appears in 3 different chains, clearly shown in the provided Path to Pillar Visualization:

  • Path 1: CWE-693 > CWE-330 > CWE-344 > CWE-798
  • Path 2: CWE-710 > CWE-657 > CWE-671 > CWE-798
  • Path 3 (Primary): CWE-284 > CWE-287 > CWE-1390 > CWE-1391 > CWE-798

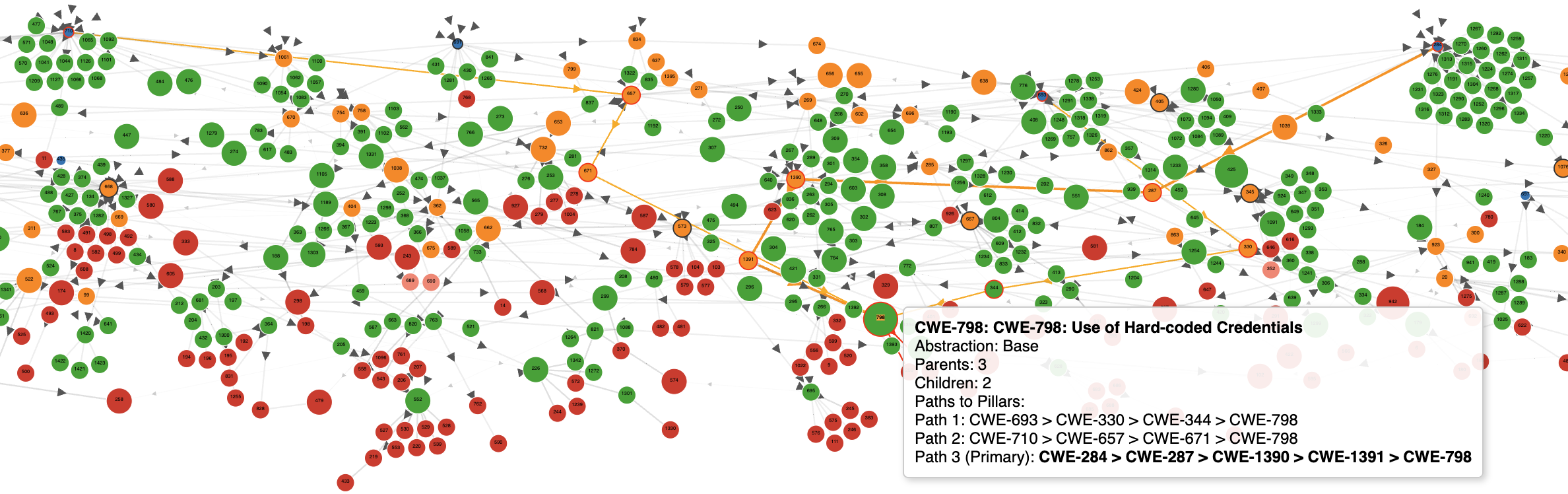
CWE-798 appears in 3 different chains. Only one path is the primary path.

Info

This raises the question of which chain(s) do we use

  • the shortest chain?
  • all the chains?
  • a selected chain?

For all chains: - the logic is the same always - the Recall and F1 will be lower if the CWE that appears in multiple chains is in the Predicted set

For CWEs with multiple parents, the “best” answer for mapping is the Primary parent and path*.

  • Each weakness can have one and only one ChildOf relationship that’s labeled “Primary” for each view.

Using all 3 chains for CWE-798:

  • Benchmark: CWE-912, CWE-798
  • Prediction: CWE-321, CWE-912

Chains used (excluding CWE-1000 Root):

  • CWE-912 Chain: CWE-710 > CWE-684 > CWE-912

  • CWE-798 Chains:

  • Chain 1: CWE-693 > CWE-330 > CWE-344 > CWE-798

  • Chain 2: CWE-710 > CWE-657 > CWE-671 > CWE-798
  • Chain 3 (Primary): CWE-284 > CWE-287 > CWE-1390 > CWE-1391 > CWE-798
  • CWE-321 Chain: CWE-284 > CWE-287 > CWE-1390 > CWE-1391 > CWE-798 > CWE-321

Augment sets:

  • Benchmark (Y):

  • CWE-912 ancestors: {CWE-710, CWE-684}

  • CWE-798 ancestors (all chains): {CWE-693, CWE-330, CWE-344, CWE-710, CWE-657, CWE-671, CWE-284, CWE-287, CWE-1390, CWE-1391}
  • Y_aug = {CWE-912, CWE-798, CWE-710, CWE-684, CWE-693, CWE-330, CWE-344, CWE-657, CWE-671, CWE-284, CWE-287, CWE-1390, CWE-1391}

  • |Y_aug| = 13

  • Prediction (Ŷ):

  • CWE-321 ancestors: {CWE-798, CWE-1391, CWE-1390, CWE-287, CWE-284}

  • CWE-912 ancestors: {CWE-710, CWE-684}
  • Ŷ_aug = {CWE-321, CWE-912, CWE-798, CWE-1391, CWE-1390, CWE-287, CWE-284, CWE-710, CWE-684}
  • |Ŷ_aug| = 9

Calculate metrics:

  • Intersection: {CWE-912, CWE-798, CWE-710, CWE-684, CWE-284, CWE-287, CWE-1390, CWE-1391} (|Intersection| = 8)
  • Precision (hP): \(\frac{8}{9} \approx 0.889\)
  • Recall (hR): \(\frac{8}{13} \approx 0.615\)
  • F-score (hF): \(\frac{2 \times 0.889 \times 0.615}{0.889 + 0.615} \approx 0.727\)

Result: Approx. 0.727, capturing key overlaps but diluted recall due to multiple ancestor paths.

Using only the Primary Path (Chain 3):

  • Benchmark: CWE-912, CWE-798
  • Prediction: CWE-321, CWE-912

Chains used:

  • CWE-912: CWE-710 > CWE-684 > CWE-912
  • CWE-798 Primary only: CWE-284 > CWE-287 > CWE-1390 > CWE-1391 > CWE-798
  • CWE-321: CWE-284 > CWE-287 > CWE-1390 > CWE-1391 > CWE-798 > CWE-321

Augment sets:

  • Benchmark (Y):

  • CWE-912 ancestors: {CWE-710, CWE-684}

  • CWE-798 ancestors (Primary path): {CWE-284, CWE-287, CWE-1390, CWE-1391}
  • Y_aug = {CWE-912, CWE-798, CWE-710, CWE-684, CWE-284, CWE-287, CWE-1390, CWE-1391}

  • |Y_aug| = 8

  • Prediction (Ŷ) (same as above): {CWE-321, CWE-912, CWE-798, CWE-1391, CWE-1390, CWE-287, CWE-284, CWE-710, CWE-684}

  • |Ŷ_aug| = 9

Calculate metrics:

  • Intersection (same as before): |Intersection| = 8
  • Precision (hP): \(\frac{8}{9} \approx 0.889\)
  • Recall (hR): \(\frac{8}{8} = 1.0\)
  • F-score (hF): \(\frac{2 \times 0.889 \times 1.0}{0.889 + 1.0} \approx 0.941\)

Result: Approx. 0.941, higher recall from narrower focus on primary path.

Using one non-primary path (Chain 1: CWE-693 > CWE-330 > CWE-344 > CWE-798):

  • Benchmark: CWE-912, CWE-798
  • Prediction: CWE-321, CWE-912

Chains used:

  • CWE-912: CWE-710 > CWE-684 > CWE-912
  • CWE-798 (Non-primary): CWE-693 > CWE-330 > CWE-344 > CWE-798
  • CWE-321: CWE-284 > CWE-287 > CWE-1390 > CWE-1391 > CWE-798 > CWE-321

Augment sets:

  • Benchmark (Y):

  • CWE-912 ancestors: {CWE-710, CWE-684}

  • CWE-798 ancestors (Chain 1): {CWE-693, CWE-330, CWE-344}
  • Y_aug = {CWE-912, CWE-798, CWE-710, CWE-684, CWE-693, CWE-330, CWE-344}

  • |Y_aug| = 7

  • Prediction (Ŷ) (same as above): |Ŷ_aug| = 9

Calculate metrics:

  • Intersection: {CWE-912, CWE-798, CWE-710, CWE-684} (|Intersection| = 4)
  • Precision (hP): \(\frac{4}{9} \approx 0.444\)
  • Recall (hR): \(\frac{4}{7} \approx 0.571\)
  • F-score (hF): \(\frac{2 \times 0.444 \times 0.571}{0.444 + 0.571} \approx 0.500\)

Result: Approx. 0.500, significantly lower, highlighting sensitivity to chosen paths.

Summary of Results

Scenario Precision (hP) Recall (hR) F-score (hF)
All 3 Chains 0.889 0.615 0.727
Primary Path Only 0.889 1.000 0.941
Non-primary Path (Chain 1) 0.444 0.571 0.500

This clearly demonstrates how significantly path selection affects scoring. Using the primary path achieves the highest performance by aligning predictions with the benchmark’s primary hierarchical representation.

Example 8: "Similar CWEs" Prediction on a Different Branch

CWE-125: Out-of-bounds Read and CWE-476: NULL Pointer Dereference conceptually share high-level similarities (both being related to memory handling errors)

Paths to Pillars CWE-125: Out-of-bounds Read

  • Path 1 (Primary): CWE-664 > CWE-118 > CWE-119 > CWE-125

Paths to Pillars CWE-476: NULL Pointer Dereference

  • Path 1 (Primary): CWE-710 > CWE-476
  • Path 2: CWE-703 > CWE-754 > CWE-476

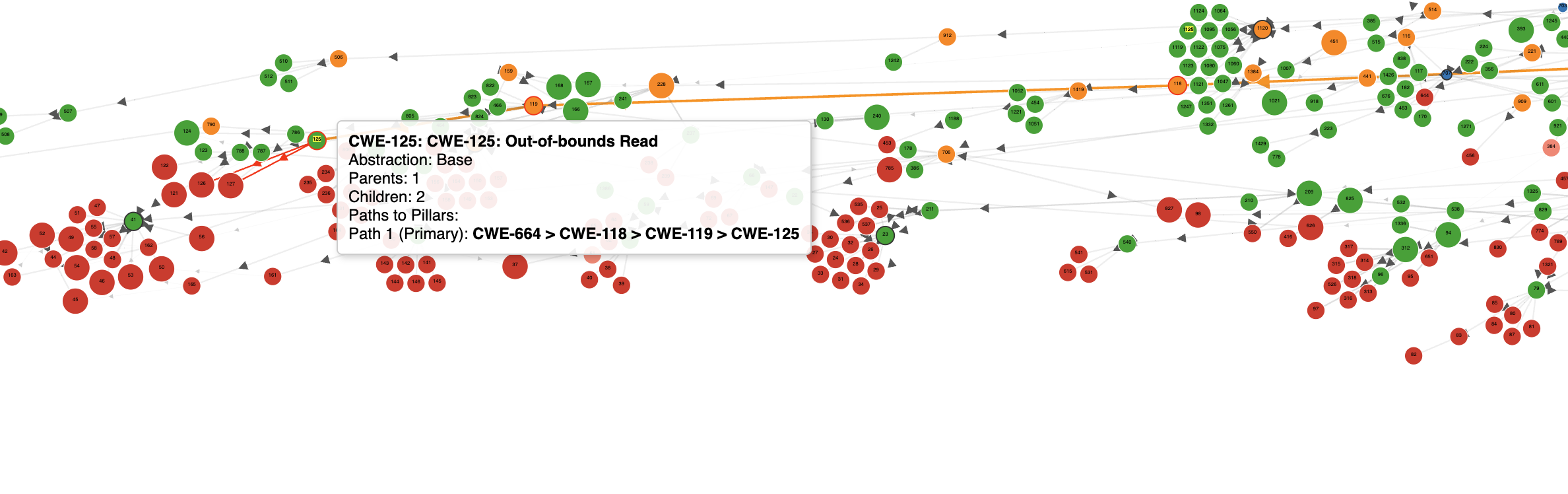
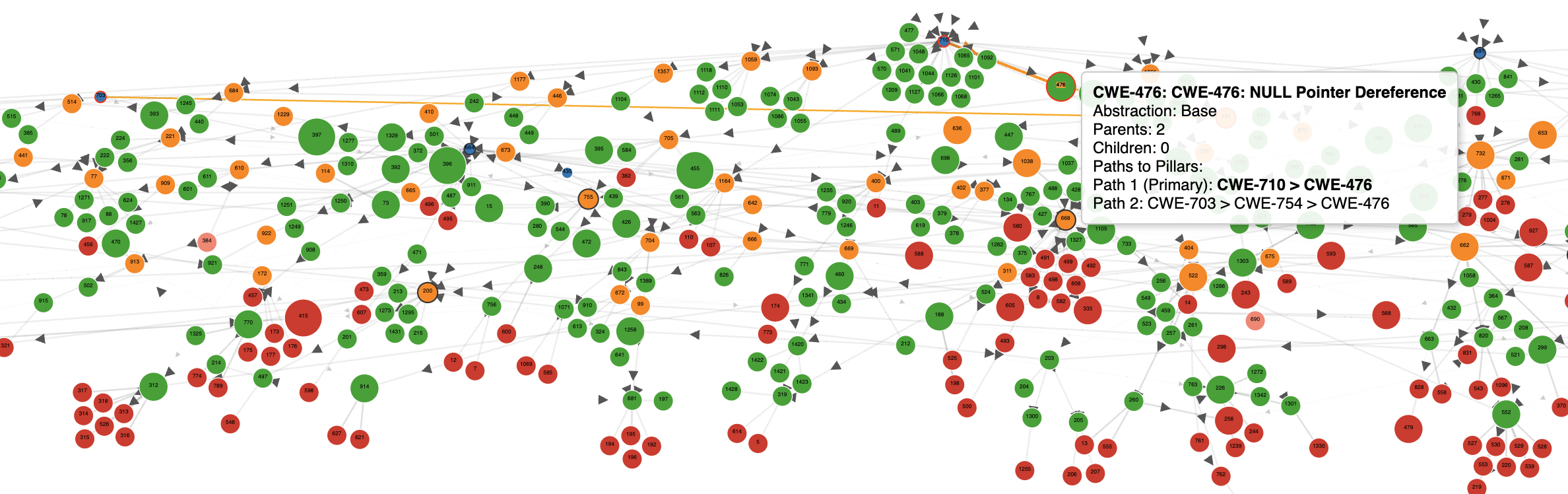
Calculate metrics:

  • Intersection: Empty set (no common ancestors between CWE-125 and CWE-476 paths)
  • Precision (hP): 0.0
  • Recall (hR): 0.0
  • F-score (hF): 0.0

Info

These two CWEs conceptually share high-level similarities (both being related to memory handling errors), but strict hierarchical scoring will not award any partial credit unless they explicitly share ancestors within the defined hierarchy.

5. Advantages of HCSS

  1. Theoretical Grounding: Based on established research in hierarchical multi-label classification
  2. Semantic Awareness: Incorporates the CWE hierarchy structure to reward closeness
  3. Balanced Evaluation: Captures both precision and recall aspects
  4. Interpretable: Produces normalized scores in a meaningful range
  5. Flexibility: Supports both micro and macro averaging for different analysis needs
  6. Standardized: Aligns with scientific evaluation practices for comparable results

6. Implementation Recommendations

  1. Use the MITRE CWE XML data to build the hierarchy graph
  2. Consider implementing optional weights for edges based on abstraction levels
  3. Provide both micro and macro-averaged scores for comprehensive evaluation
  4. Include standard metrics alongside HCSS for comparative context

This HCSS framework provides a robust, theoretically sound approach to evaluating automated CVE-to-CWE assignments, directly addressing the multi-label and hierarchical nature of the problem.